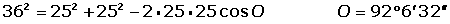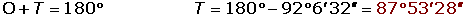LEY DE SENOS Y COSENOS

LEY DE SENOS Y COSENOS

INTRODUCCION

Teorema o ley del seno

Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.

Ejercicios

De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Determina los restantes elementos.

Teorema o ley del coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Ejemplos

Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.

El radio de una circunferencia mide 25 m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud 36 m.

CONCEPTOS TRIGONOMETRIA

CONCEPTOS TRIGONOMETRIA

ANGULO: Es la superficie que se forma con dos semirectas formando un vértice

Clasificación de ángulos según las medidas

RECTO: Es aquel que se forma con dos semirectas perpendiculares formando un ángulo de 90º.

Cuando el ángulo mide menos de 90º grados es agudo y cuando mide más de 90º es obtuso. Ejemplo:

Angulos Complementarios

Son aquellos que al ser sumados me dan o forman un angulo recto.

25º + 65º = 90º

Angulos Suplementarios

Al sumarlos forman un angulo llano.

Angulos Consecutivos

Siempre estan unidos por un vertice y comparten uno de sus lados.

Angulos unidos por el vertice.

Triangulo

Es un poligono que tiene tres lados, tres angulos y tres vertices

a, b, c = lados

A,B,C= Vertices

α,ϴ,β= Angulos

Clasificacion de los triangulos por sus lados:

·         Hay tres tipos de Angulos dependiendo de la medida de sus lados

·         EQUILATERO: Es aquel triangulo que tiene todos sus lados iguales

·         ISOSCELES: Es aquel triangulo que tiene dos lados iguales

·         ESCALENO: Es aquel triangulo que todossus lados son desiguales

Clasificacion de los triangulos por sus angulos

·         Hay tres tipos de angulos

·         Acutangulos: Es aquel triangulo donde todos sus angulos son agudos (osea miden menos de 90º)

Rectangulo: Es aquel que uno de sus angulos es recto, osea mide 90º

Obtusangulo: Es aquel que uno de sus anguloses obtuso oseamide mas de 90º

¿Cuántos angulos agudos como maximo puede tener un triangulo? R: 3

¿Cuántos angulos obtusos como maximo puede tener un triangulo? R: 1

¿Cuántos angulos agudos como maximo puede tener un angulo? R:2

¿Cuántos suman los angulos agudos de un triangulo rectangulo? R:90º

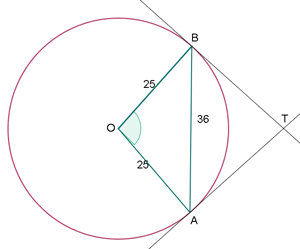
TEOREMA DE LOS TRIANGULOS

1.    Teorema: Los angulos internos de un triangulo suman 180º

2.    Teorema: Los angulos externos de un triangulo suman 360º

3.    Teorema: Un angulo externo del triangulo es la suma de la medida de los dos angulos internos cercanos a el.

·         Puntos notables de los triangulos:

Mediatriz: Es una linea perpendicular que sale del punto medio de cualquiera de los lados.

Altura: Es la linea perpendicular a dicho lado que pasa por el vertice opuesto.

Mediano: Es la recta que une el vertice con el punto medio al lado opuesto.

Bicetriz: Es una linea que sale del vertice del angulo formando dos angulos iguales.

Sistema de Medida Angular

Sexagecima: Una vuelta significa 360º

Centesimal: Una vuelta equivale a 400º

Radical o circular: Una vuelta equivale a 2π radial

Forma Incompleja – Forma Compleja

Grados sexagesimal – grados- minutos – segundos

                                        Horas – minutos – segundos

1Grado = 60`(minutos)

1Minuto = 60” (segundos)

1Hora = 3600” (segundos)

Convertir 16,5125º sexagecimales a grados, minutos y segundos.

16º

0,5125º x 60= 30`(minutos)

0,75 min x 60” seg = 45 seg

https://www.youtube.com/watch?v=lz6Y2fPq-SQ

https://www.google.com.co/search?q=suma+sistema+hexadecimal&espv=2&biw=1366&bih=667&source=lnms&tbm=isch&sa=X&ved=0CAYQ_AUoAWoVChMIy9T1orqOyQIVgsImCh1HMgKE&dpr=1#imgrc=0TG0Za9Pe_yw5M%3A

PRODUCTOS NOTABLES

1.   BINOMIO CUADRADO

·         Suma (a+b)² = a² +2ab + b²

EJ:

(3x + 2y)² = (3x)² + 2(3x) (2y) + (2y)²

                = 9x² +12xy +4y²

·         Resta (a+b)² = a² - 2ab + b²

EJ:

(8m – 5)² = (8m)² – 2 (8m) (5) + (5)²

              = 64m² – 80m + 25

2.   SUMA Y DIFERENCIA DE CUADRADOS (a + b) (a-b) = a² – b²

EJ:

(7x +3y) (7x – 3y) = (7x)² – (3y)²

                           = 49x² – 9y²

3.   BINOMIO AL CUBO

·         Suma (a +b)³ = a³ + 3a²b + 3ab² + b³

EJ:

(2m + 6)³= (2m)³ + 3(2m)²(6) + 3(2m) (6)²+ (6)³

              = 8m³+ 72m² + 216m +216

·         Resta (a - b)³ = a³ - 3a²b + 3ab² - b³

EJ:

(4m – 2n)³= (4m)³ – 3(4m)²(2n) + 3(4m) (2n)² – (2n)³

               = 64m³ – 96m²n + 48mn² – 8n³

4.   TRINOMIO AL CUADRADO

(a +b + c)² = a² +b² + c² + 2ab + 2ac +2bc

EJ:

(2x + 3y – 5z)²= (2x)²+ (3y)²+ (-5z)²+ 2(2x) (3y) + 2(2x) (-5z) + 2(3y) (-5z)

                       = 4x² +9y² + 25z² + 12xy -20xz -30yz

5.   SUMA DE CUBOS

a³ + b³= (a +b) (a² – ab +b²)

EJ:

64m³ + 125n⁶ = (4m + 5n²) {(4m)² – (4m) (5n²) + (5n²)²}

                     =(4m + 5n²) (16m² – 20mn² + 25n⁴)

6.   DIFERENCIA DE CUBOS

a³ – b³ = (a- b) (a²+ab+b²)

EJ:

27x¹² – 8y⁹= (3x⁴ – 2y³) {(3x⁴)² + (3x⁴) (2y³) + (2y³)²}

                = (3x⁴ – 2y³) (9x⁸ + 6x⁴y³+ 4y⁶)

7.   TRIENGULO DE PASCAL

(a + b)⁴= 1a⁴ +4a³b + 6a²b² +4ab³ + 1b⁴

(2x – 3y)⁴= 1(2x)⁴ – 4(2x)³ (2y) + 6(2x)²(3y)² – 4(2x)(3y)³ +1(3y)⁴

               = 16x⁴ – 96x³y +216x²y² -216xy³ + 81y⁴

FACTORIZACION

1. FACTOR COMUN MONOMIO - POLINOMIO

EJ. 1:

12x + 18y - 24z 

= (6) (2x + 3y - 4z)

EJ.2:

24a - 12ab

= (12a) (2-b)

2. FACTOR COMUN AGRUPANDO TERMINO:

EJ:

2am - 4an - bm + 2bn

= 2a (m - 2n) - b (m - n)

= (2a - b) (m - 2n)

3. TRINOMIO CUADRADO PERFECTO

1. Tiene que tener tres términos

2. Tiene que tener raíz el primer y tercer termino

3. multiplicar las 2 raices por dos y debe dar como resultadoelsegundo termino

EJ:

9x^{2 - 30x + 25}

4. TRINOMIO DE LA FORMA x² + bx +c

1. siempre debe ir cualquier literal acompañado de 1

2. Se abren dos paréntesis y se coloca raiz del primer termino en los dos parentesis

3. En el primer factor debe ir el el signo del segundo termino

4. Ley de los signos entre el segundo y tercer termino

5. buscar dos numeros que multiplicados le den el tercer termino y que sumados o restados me den el segundo termino

EJ:

x² + 6x + 5

= (x + 5) (x + 1)

5.TRINOMIO DE LA FORMA ax² + bx +c

 1. multiplicar todos los terminos por el primer termino

2.Se multiplica odesarrolla el primero y el tercer termino y el segundo queda igual

3. abrir 2 parentesis y colocar raiz cuadrada del primer termino en cada parentesis

4. buscar 2 numeros que multiplicados me den el tercer termino y que sumados o restados me den el segundo termino

EJ:

2x² – 11x + 5

2x² (2) – 11x (2) + 5 (2)

=4x² – 11x (2) + 10

= (2x- 10) (2x – 1)

_____________________

           2 . 1

= (x -5) (2x – 1)